あ,ども,こんにちは.
今日はですね,最近学び始めている非定常拡散方程式をpythonをつかってグラフにしていきます.
まぁ,なんというか,自分の学んだことをどうにかして残さないとと思ったので書きます笑
さらに解の安定性についても考察するのでご覧くださいな.
数式の確認
今回対象とする方程式はこちら.一次元非定常拡散方程式です.
\[
\frac{\partial u}{\partial t} = k\frac{\partial^2 u}{\partial^2 x}
\]
位置はxのみなので,1次元.時間による変化があるので非定常です.
また,右辺が拡散項となっており,kが拡散係数.
差分化
差分化について詳しく述べることはしません.
今回は陽解法である,前進オイラー法を用います.
\[ u_{i}^{n+1} = u_{i}^n + k\frac{\Delta t}{\Delta x^{2}}\{u_{i+1} – 2u_{i} + u_{i-1}\} \]
また,境界条件,初期条件はこんな感じにしましょう.
\[
0<x<1 \\
u_{x}^0 = -20x(x-1) \\
u_{0}^t,u_{1}^t = 1
\]
pythonで書く
ここではコードを載せるだけ笑
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
# 初期値
k = 1
L = 1
N = 31
dx = L/N
T = 100
dt = 0.001
u = np.zeros((T,N)) #全てに0を入れておく
for t in range(0,T):
for x in range(0,N-1):
if t == 0:
u[t][x] = -20*x*dx*(x*dx-1)
else:
if x == 0 or x == N-1:
u[t][x] = 0
else:
u[t][x] = k*dt/(dx**2)*(u[t-1][x+1]-2*u[t-1][x]+u[t-1][x-1]) + u[t-1][x]
plt_x = np.linspace(0,L,N)
fig = plt.figure()
ims = []
for i in range(0,T):
im = plt.plot(plt_x,u[i],color='#4169e1')
ims.append(im)
ani = animation.ArtistAnimation(fig, ims, interval=200)
plt.show()Code language: PHP (php)こんな感じ.勝手にアニメーションのグラフができるようになっている.

安定性について
僕が話したかったのはここです笑
上で見せたグラフはいい感じになっていますが,例えば要素分割数をN=21からN=31に変えるとt=5*dtの時には,こんな感じになりました.
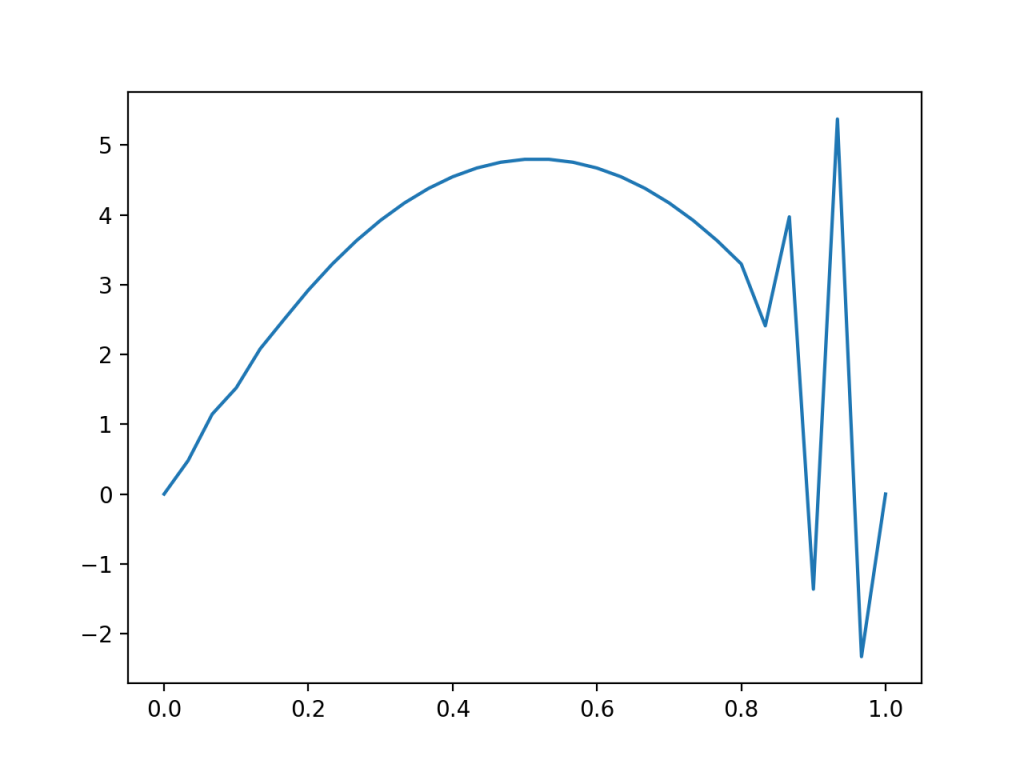
大変な振動が起こってしまっています.
これをちょっと検討していきたいというのが今日のお話です.
メッシュ数を増やしたのに...
そうです,メッシュ数はあった方が精度が高くなりそうと考えていたのにも関わらず,こんなに振動してしまう結果となりました.
安定条件
先に今回の安定条件を示しておくと,
\[
r=k\frac{\Delta t}{\Delta x^{2}} \leq \frac{1}{2}
\]
となります.実はこのr,N=21の時は0.441だったのですが,N=31の時は0.961と0.5を超えてしまっています.安定条件を満たしていなかったので,こんなにも振動してしまっていたのですね.
安定条件とは?
さて,先ほどの安定条件を示す式がどこからでてきたのかっていうのが気になるところですよね.
以下から安定条件の考え方を示します.
流れとしては,特解を導き発散条件を確認します.
特解の仮定
\[ u_{i}^{n+1} = u_{i}^n + k\frac{\Delta t}{\Delta x^{2}}\{u_{i+1} – 2u_{i} + u_{i-1}\} \]
この式(用いた差分式)は
\[ r = k\frac{\Delta t}{(\Delta x)^2} \\
u_{i}^{n+1} = r u_{i-1}^{n}+(1-2r)u_{i}^{n}+r u_{i+1}^{n} \]
とすることができる.この差分方程式の特解を下記のように仮定する.
\[ u_{i}^{n} = g^{n}\exp(\sqrt(-1 \xi j \Delta x)) \]
この仮定した解を差分方程式に両辺に代入して解くと
\[ g = 1-4sin^2(\frac{\xi \Delta x}{2}) \]
となる.これを満たせていれば仮定した特解は満足していることとなる.
特解から検討
ここで,仮定した特解を見直すと,gの絶対値が1を超える場合,nが大きくなるほどuが発散してしまう.
そのため,uが発散しない条件は,
\[ r \leq \frac{1}{2} \]
となります.(細かい計算は端折っているので試してみてください.)
参考文献
- 中島研吾「偏微分方程式の数値解法」(http://nkl.cc.u-tokyo.ac.jp/13n/PDE.pdf)
- 河村哲也「流体解析の基礎」(朝倉書店)



コメント