えー,どうも,こんにちは.
はじめに
流体計算というのは多く存在しますが,その中の一つ,水.
流体計算の中でも難しい印象にありますね.その理由としては粘性であること,それから非圧縮性流体であることが挙げられると思います.
流体の基本はナビエ・ストークス方程式に基づきますが,水の流れに着目するとz軸の流れに対し,x,y軸の流れが卓越していることが多いです.そこで用いられるのが「浅水流方程式」です.
今回はこの「浅水流方程式」を1次元で離散化し,簡単な段波のシミュレーションを行います.
数式
1次元浅水流方程式
今回扱う式は以下の二つの式になります.
ただし今回は標高差はないと仮定します.
\[
\frac{\partial h}{\partial t} + \frac{\partial uh}{\partial x} = 0
\]
\[
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = – g \frac{\partial h}{\partial x} – \frac{g n^2u\left|u\right|}{h^{(4/3)}}
\]
ここでhは水深で,uは平均流速になります.gは重力加速度,nはマニングの粗度係数です.
上の式が一般に連続式と呼ばれていて,下の式が運動量式と呼ばれています.
下の運動量式について簡単に説明をすると,
- 左辺第1項→時間項(たぶん)
- 左辺第2項→移流項
- 右辺第1項→圧力項
- 右辺第2項→粘性項
と呼ばれていますね.
簡略化
さて,今回はしきを簡単にするためマニングの粗度係数n=0とします.粘性が全くない理想流体として考えるということです.
すると,運動量式のみ変わっていますが,
\[
\frac{\partial h}{\partial t} + \frac{\partial uh}{\partial x} = 0
\]
\[
\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = – g \frac{\partial h}{\partial x}
\]
離散化
では上の方程式を離散化していきます.
まずは,連続式.
時間方向に前進差分,x方向に中央差分でいきます.
\[
h^{n+1}_i = -\frac{dt}{2dx}(u^{n}_{i+1}h^{n}_{i+1} – u^{n}_{i-1}h^{n}_{i-1}) + h^{n}_{i}
\]
続いて,運動量式
先程と同様に時間方向に前進差分,それから移流項には1次風上差分を,圧力項には中央差分としました.
ここで注意して欲しいのが,移流項です.今回は後ほど説明する条件もあり,流速はx方向に正としています.他の問題を扱う場合にはここが変わってきます.
\[
u^{n+1}_i = -\frac{dt}{dx}u^{n}_{i}(u^{n}_{i}-u^{n}_{i-1}) + u^{n}_{i} – g \frac{dt}{2dx}(h^{n}_{i+1} – h^{n}_{i-1})
\]
シミュレーション
ダムブレーク問題(初期条件)
さて,今回は参考文献を見ながらダムブレーク問題について見ていきたいと思います.これは実は浅水流方程式で解くことについて問題視されていて,それを題材にした論文が一つ目の参考文献なのです.
結果を見ると問題視される理由もわかると思うのでこのまま考えていきましょう.
さてダムブレーク問題では水槽の真ん中にアクリル板があって,アクリル板の左には水がたくさん,アクリル板の右には水が全くない状態を初期状態とします.
このアクリル板を一瞬にして取り除いたらどうなるかというのがダムブレーク問題になります.
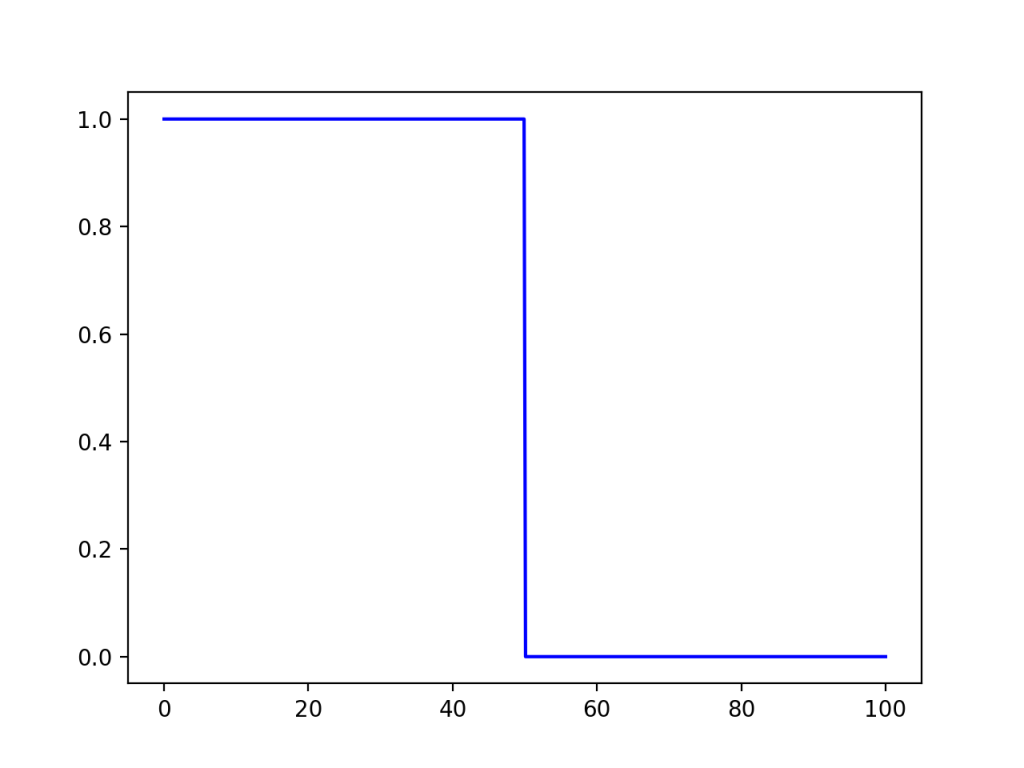
今回は図のように水がある部分には1mの水深を,そうでないところには0mの水深を与えています.x軸は0~100mで考えて,アクリル板の位置はx=50mとしました.
イメージとして,計算をすると(アクリル板を外すと)水がアクリル板の右に行くことは容易に想像できます.そのため流速は正の方向と仮定しています.
計算条件
さて,計算条件ですね.
- 格子分割数(nx) = 500[m]
- 計算単位時間(dt) = 0.005[s]
- 計算最大時間(tmax) = 2000[s](dt*tmax = 10秒後まで計算することとなる)
まぁ,このくらいかな.詳しくは後ほど書くプログラムを見てください.
境界条件
- x=0において,u=0,h=1
- x=100において,u=0,h=0
としました,あとは特にって感じですね.
計算開始!
コード(python)
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
nx = 500
dx = 100/nx
dt = 0.005
tmax = 2000
g = 9.81
u = np.zeros((tmax,nx))#流速
h = np.zeros((tmax,nx))#水深
h[0:tmax,0:nx//2] = 1
x_axis = np.linspace(0,100,nx)
for tt in range(tmax-1):
for xx in range(1,nx - 1):
u[tt+1,xx] = -dt/dx * u[tt,xx]*(u[tt,xx]-u[tt,xx-1]) + u[tt,xx] - g*dt/(2 * dx)*(h[tt,xx+1] - h[tt,xx-1])
for xx in range(1,nx - 1):
h[tt+1,xx] = -dt/(2*dx)*(u[tt,xx+1]*h[tt,xx+1] - u[tt,xx-1]*h[tt,xx-1]) + h[tt,xx]
#こっから先は最後に表示する方法で,動画として見せるもの,画像として特定の時間のグラフを見せるものを用意しています
def exportMovie():
fig = plt.figure()
ims = []
for tt in range(tmax):
im = plt.plot(x_axis,h[tt],"blue")# 乱数をグラフにする
ims.append(im)# グラフを配列 ims に追加
# 10枚のプロットを 100ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=5)
plt.show()
def exportPicture(time):
plt.plot(x_axis,h[time],"blue")# 乱数をグラフにする
plt.show()
#どちらかでいい
exportPicture(0)
# exportMovie()
Code language: Python (python)とりあえずこんな感じ.下の二つの関数は表示ようなのであまり気にしないで欲しい.
気をつけて欲しいところとしては,流速も水深もx=1~nx-1までしか計算していない.これは境界条件の考慮のためです.
まぁこんな感じかな.
計算結果
簡単な考察
これ,動画を見るとわかりますが,流れの先端が段になってしまっています.これを段波といいます.
これは明らかに現実とはかけ離れていますよね.この段波の原因として浅水流方程式は流れの方向に水があることを前提にしていることが挙げられます.
参考文献にある論文はこれを解決するためにどうするのか,という部分について研究を進めているのでぜひそちらも見てみてください.
また,この計算は10秒後までしかシミュレーションしていませんが,水の流れが逆方向になると変な結果になってしまうので,ご注意ください.
参考文献
楊宏選,陸 旻皎,熊倉俊郎:浅水流方程式の先端の扱いに関する研究(2016)


コメント